I statistikk er vi veldig ofte i en situasjon hvor vi er interessert i å relatere et sett med mulige forklaringsvariabler til en responsvariabel. Da er regresjonsanalyse et fornuftig verktøy. Regresjonsanalyse tilhører arbeidshestene i den statistiske verktøykassen og har et stort bruksområde.
De fleste som har hatt noe statistikkundervisning har et forhold til lineær regresjonsanalyse, da dette undervises i de aller fleste innføringskurs i statistikk. Metoden benyttes når responsvariabelen måles på en kontinuerlig skala. Modellen kan skrives som følger:
y = β0 + β1x1 + β2x2 + … + βpxp + ε .
Her er y vår responsvariabel, x1,…xp er et sett med p forklaringsvariabler, β0, β1,…βp er våre regresjonskoeffisienter, det vi er ute etter å estimere, og ε betegner modellfeilen. Regresjonskoeffisientene β1,…βp gir oss sammenhengen mellom de enkelte forklaringsvariablene x1,…xp og responsvariabelen y.
I medisin er vi ofte interessert i binære responsvariabler, altså variabler med to mulige verdier, typisk syk/ikke syk. Som et eksempel kan vi tenke oss at vi er interessert i effekten av systolisk blodtrykk på risikoen for død av hjerte- og karsykdommer, hvor vi registrerer død ved en ja/nei variabel. Den mest brukte regresjonsmodellen for denne typen responser er logistisk regresjon. Lineær regresjon og logistisk regresjon har mange fellestrekk, men også enkelte fundamentale forskjeller.
Oddsforholdet
I en logistisk regresjonsmodell er vi ute etter å modellere sannsynligheten for responsen vår, f.eks. sannsynligheten for sykdom. La oss betegne denne sannsynligheten med p. I den logistiske modellen antar vi at vi kan modellere p som en funksjon av våre forklaringsvariabler x1,…xp på følgende vis:
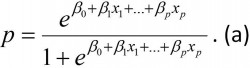
Legg merke til at p nå alltid vil ligge mellom 0 og 1, som vi vil ønske. Ved å flytte litt om på ligningen over kan den også uttrykkes som
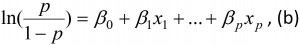
hvor ln-funksjonen betegner den naturlige logaritmefunksjonen med grunntall e. Størrelsen p/(1-p) kalles for odds, og funksjonen ln(odds) kalles ofte for logit-funksjonen. Nå ser vi likheten med den lineære regresjonsmodellen, ved at høyresiden av regresjonsligningen er en lineær funksjon av forklaringsvariablene. Vi ser imidlertid også en klar forskjell, nemlig at regresjonskoeffisientene ikke direkte gir sammenhengen mellom forklaringsvariablene våre og responsen, siden venstresiden i ligningen ikke er vår responsvariabel y, men ln(p/(1-p)). Vi må dermed gjøre en transformasjon av regresjonskoeffisientene for å få noe som er tolkbart.
La oss tenke oss en enkel situasjon med én enkelt forklaringsvariabel x, og la x ta verdiene 0 og 1 (ikke-eksponert versus eksponert). I eksemplet vårt med blodtrykk og død av hjerte- og karsykdommer kan vi tenke på dette som at man er eksponert dersom man har et systolisk blodtrykk over 140 mm Hg og ikke-eksponert ved verdier under 140 mm Hg. Først ser vi at ved å bruke eksponentialfunksjonen på begge sider av likhetstegnet får vi
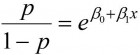
hvor p/(1-p) altså er oddsen for responsen vår. For x = 1 blir oddsen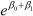 
, mens for x = 0 blir oddsen 
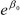. Forholdet mellom disse to størrelsene blir da oddsforholdet (OR), et mye brukt effektmål, og vi ser at vi sitter igjen med 
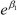siden
.
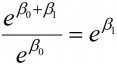Altså, i logistisk regresjon er vårt naturlige effektmål ikke regresjonskoeffisienten β, men eβ siden dette gir oss oddsforholdet.
La oss anta at dataene gir en estimert regresjonskoeffisient på 0,81. Da har vi OR = e0.81 = 2,25, som sier at oddsen for død av hjerte- og karsykdommer er 2,25 ganger høyere om man har et systolisk blodtrykk over 140 mm Hg enn om man ligger under 140 mm Hg. Alle standard statistikkpakker vil kunne gi resultatene av en logistisk regresjonsmodell i form av OR med tilhørende konfidensintervall.
Estimert risiko
For mange er imidlertid oddsbegrepet vanskelig å forholde seg til, og også det at vi opererer med et såkalt relativt effektmål (et forhold) kan være problematisk. Det vil dermed kunne være av interesse å se mer direkte på hvordan forklaringsvariabelen, systolisk blodtrykk, påvirker risikoen for respons, død av hjerte- og karsykdommer. Dette kan gjøres ved å ta tak i formuleringen (a). La oss anta at vi er interessert i effekten av blodtrykk målt på kontinuerlig skala, og at vi finner en estimert β0 på -8,87 og en estimert β1 på 0,036. Den siste størrelsen her angir effekten av systolisk blodtrykk og kan oversettes til en OR ved å ta e0.036 = 1,04. Dette angir altså effekten av å øke blodtrykket med 1 mm Hg. Mer relevant er det kanskje å studere effekten av å øke blodtrykket med 10 mm Hg. Denne effekten får vi enkelt ved å beregne e10·0.036 = 1,43. La oss nå se hvordan vi kan utnytte (a). Vi har kun én forklaringsvariabel x, så (a) blir seende ut som
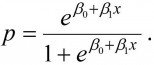
Nå kan vi for eksempel sette inn medianverdien av systolisk blodtrykk, som i vårt materiale er 133 mm Hg, sammen med våre estimerte verdier av β0, β1 og vi får en estimert risiko for død av hjerte- og karsykdommer på
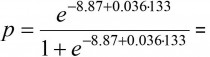
0,017, eller 1,7 %. Hvordan endrer denne estimerte risikoen seg hvis vi øker blodtrykket til 143 mm Hg, som tilsvarer 75-prosentilen i vårt materiale? Da gjør vi den samme utregningen, men med x = 143, og vi finner en estimert risiko på 0,024, eller 2,4 %. Dette illustrerer altså hvilken effekt blodtrykk har på risikoen for død av hjerte- og karsykdom.
Logistisk regresjon er svært anvendelig og er mye brukt til å analysere kliniske og epidemiologiske data, også av forskere med begrenset erfaring med statistisk modellering. Metoden er lett tilgjengelig i standard programvare. Dersom du er interessert i å lese mer om logistisk regresjon, finner du en mer utfyllende introduksjon i kapitlet til Veierød & Laake (1), mens man i boken Applied logistic regression gir en fullstendig behandling av temaet (2).
