Helsemyndighetene kommer med en rekke anbefalinger, for eksempel vedrørende livsstil, for å bedre helsetilstanden i befolkningen. Slike anbefalinger bygger i stor grad på observasjonelle studier, som er beheftet med konfunderingsproblemer.
Innen medisinsk forskning blir randomiserte, kontrollerte studier sett på som gullstandarden. Eksempelvis vil man ikke kunne få registrert et nytt legemiddel uten at det har vært igjennom et antall slike studier. Grunnen til at de randomiserte studiene har en slik posisjon er at man gjennom randomiseringen sikrer at gruppene som man sammenligner, er relativt like med hensyn til alle andre faktorer (kjønn, alder, osv.) enn akkurat den eksponeringen man er ute etter å sjekke effekten av.
Dersom man da finner en forskjell mellom gruppene angående utfallsvariabelen, er det rimelig å konkludere med at dette skyldes eksponeringen. Imidlertid kan man ikke gjennomføre randomiserte studier på alle typer eksponering. Mange livsstilvariabler er av denne typen.
Det er for eksempel helt utenkelig å skulle gjennomføre en randomisert studie på røyking for å undersøke effekten når det gjelder risikoen for hjerte- og karsykdom. Her må vi stole på observasjonelle studier. Observasjonelle studier har imidlertid den store ulempen at den eksponerte gruppen (røykerne) og den ikke-eksponerte gruppen (ikke-røykerne) ikke nødvendigvis er balanserte med tanke på andre faktorer. Eksempelvis kan røykere generelt føre en mer usunn livsstil enn ikke-røykere. Dette medfører at en eventuell forskjell mellom gruppene med hensyn til risiko for sykdom ikke direkte kan tilbakeføres til den eksponeringen man studerer (røyking). Den kan like gjerne skyldes en eller flere andre faktorer som også skiller de to gruppene.
Slike faktorer, eller variabler, kaller vi konfunderende. En variabel er konfunderende for sammenhengen mellom en eksponering og et utfall dersom den påvirker både eksponering og utfall (fig 1).
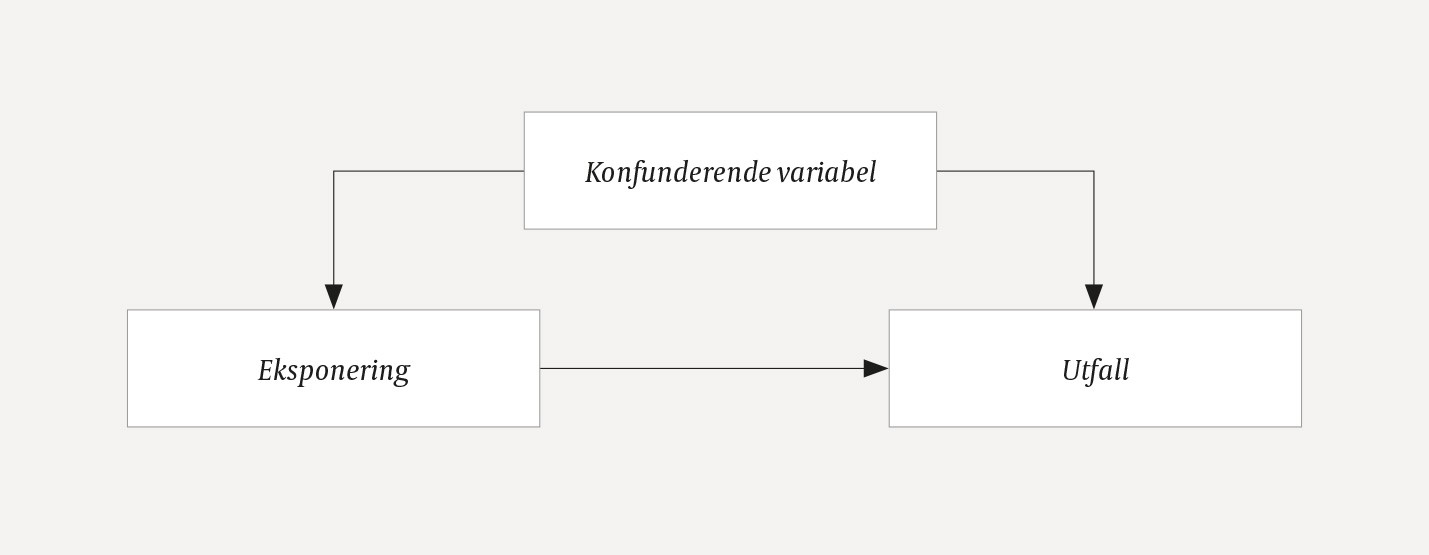
Figur 1 En konfunderende variabel påvirker både eksponering og utfall
Hvordan håndtere konfundering?
I en statistisk analyse kan man ta hånd om konfundering på forskjellige måter. Man kan gjennomføre en stratifisert analyse hvor man stratifiserer på den konfunderende variabelen, eller man kan justere for den konfunderende variabelen i en regresjonsanalyse. En stratifisert analyse vil fungere bra dersom man kun har én konfunderende variabel og denne har et begrenset antall verdier. Dersom man har flere konfunderende variabler, og en eller flere av disse er målt på en kontinuerlig skala, er det imidlertid mer naturlig å løse problemet ved å inkludere disse variablene i en regresjonsmodell, sammen med hovedeksponeringen. La oss se på et eksempel.
Vi vil studere sammenhengen mellom lungefunksjon, målt ved Peak Expiratory Flow (PEF), og høyde. Vi har data fra et kull medisinstudenter, og hvis vi setter opp en lineær regresjonsmodell for denne sammenhengen, finner vi en estimert regresjonskoeffisient på 9,6. Dette sier altså at for hver centimeter økning i høyde vil vi i gjennomsnitt øke lungefunksjonen med 9,6 l/min, eller sagt på en annen måte: Dersom vi sammenligner en gruppe studenter med en gitt høyde, f.eks. 165 cm, med en annen gruppe studenter som er 10 cm høyere, vil gruppen som er 10 cm høyere ha en gjennomsnittlig lungefunksjon som er 10 . 9,6, altså 96 l/min, høyere enn gruppen som er 165 cm.
Denne analysen tar imidlertid ikke hensyn til at de to gruppene kan variere med tanke på andre faktorer. Spesifikt tar den ikke hensyn til kjønnsforskjeller. Det er en sterk sammenheng mellom høyde og kjønn, og det er også en sammenheng mellom kjønn og lungefunksjon som går på andre parametere enn høyde. Kjønn vil derfor kunne opptre som en konfunderende faktor i analysen vår. Siden vi i dette eksemplet kun har én konfunderende faktor, og denne faktoren bare tar to verdier (kvinne og mann), kan vi bruke begge strategiene nevnt over for å ta hensyn til konfundering. La oss først gjennomføre en stratifisert analyse.
Vi analyserer altså sammenhengen mellom lungefunksjon og høyde for kvinner og menn hver for seg. For kvinner får vi da en estimert sammenheng (uttrykt ved en estimert regresjonskoeffisient) på 3,5, mens for menn blir den tilsvarende størrelsen 4,0, og man vil enten presentere disse to stratifiserte estimatene eller et vektet gjennomsnitt av dem. I vårt tilfelle vil et slikt vektet gjennomsnitt bli 3,7.
Alternativt kan vi analysere disse dataene ved å legge inn kjønnsvariabelen i regresjonsmodellen vår. Modellen blir da, veldig skjematisk, seende ut som Peak Expiratory Flow = høyde + kjønn. Gjør vi dette, finner vi en estimert effekt av høyde på 3,7, altså det samme som vårt vektede gjennomsnitt over. Fortolkningen er at dette er sammenhengen mellom høyde og lungefunksjon for en gitt verdi av kjønn, altså for enten mann eller kvinne. Vi vil altså mene at dette er et mer korrekt estimat for den «rene» effekten av høyde.
Det er verdt å bemerke at de to måtene å se dette på ikke nødvendigvis vil produsere eksakt det samme resultatet, men de bør være relativt like.
Restkonfundering
Ved disse metodene kan vi altså ta hånd om konfundering på en god måte hvis vi kjenner, og har målt, de konfunderende variablene. I praksis vil vi imidlertid nesten aldri kunne utelukke at det finnes en viss restkonfundering som vi ikke klarer å ta hånd om i analysen. I slike tilfeller kan vi gjennomføre en sensitivitetsanalyse for å få et visst begrep om hvor stor betydning en slik restkonfundering kan tenkes å ha (1).
