To leger vil ikke alltid konkludere likt når de vurderer en pasient. Cohens kappa er et mye brukt statistisk mål på samsvar.
En tidligere artikkel i spalten Medisin og tall omhandlet samsvar mellom en diagnostisk test og den faktiske tilstanden til pasienten, målt ved en gullstandard som representerer «sannheten» (1). Her skal vi se på grad av samsvar mellom observatører når man ikke kjenner fasiten. Observatørene kan for eksempel være radiologer som vurderer røntgenbilder, eller fysioterapeuter som klassifiserer motorisk funksjon.
Vi skal ta utgangspunkt i et eksempel hvor fysioterapeuter har klassifisert motorisk funksjon i hendene hos barn med cerebral parese med en femtrinns skala, der nivå I beskriver beste og nivå V dårligste funksjon (2). 79 barn ble klassifisert av fire observatører, basert på videoopptak. Tabell 1 viser resultatene for observatør A og B.
Tabell 1
Finmotorisk funksjon hos 79 barn med cerebral parese, klassifisert av to observatører, på en skala fra I (best) til V (dårligst). Data fra (2)
|
|
Observatør B
|
|
|
Observatør A
|
I
|
II
|
III
|
IV
|
V
|
Totalt
|
|
I
|
22
|
3
|
0
|
0
|
0
|
25
|
|
II
|
7
|
16
|
2
|
1
|
0
|
26
|
|
III
|
0
|
1
|
5
|
7
|
0
|
13
|
|
IV
|
0
|
0
|
1
|
8
|
1
|
10
|
|
V
|
0
|
0
|
0
|
1
|
4
|
5
|
|
Totalt
|
29
|
20
|
8
|
17
|
5
|
79
|
Cohens kappa
Et intuitivt mål på samsvar mellom observatørene kunne være andelen klassifiseringer der observatørene er enige. Det tilsvarer de klassifiseringene som ligger på «diagonalen» i tabell 1. Her er observatørene enige for 22 + 16 + 5 + 8 + 4 = 55 barn, dvs. en andel på
po = 55 / 79 = 0,70
Men noe av dette kan skyldes tilfeldigheter: La oss tenke oss at observatør A klassifiserte 25 av barna som klasse I, 26 av barna som klasse II osv., og tilsvarende for observatør B, uten å observere videoene. Da ville forventet andel samsvar bli pe = (29 · 25 + 20 · 26 + 8 · 13 + 17 · 10 + 5 · 5) / 792 = 0,25.
Cohens kappa er definert som relativt samsvar ut over tilfeldighet, nærmere bestemt
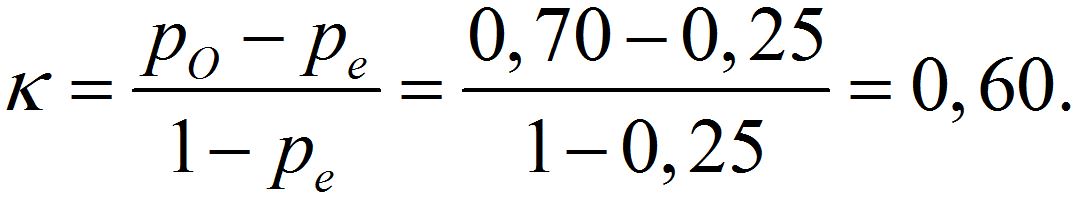
Cohens kappa vil bli 1 ved perfekt samsvar og 0 ved samsvar som er like dårlig som å kaste «mynt og kron». En verdi under 0 ville tyde på dårligere samsvar enn ved tilfeldighet, noe som sjelden er tilfelle. Det er uansett viktig å rapportere krysstabellen som ligger til grunn, og ikke bare verdien av kappa.
Vektet kappa ved ordinal klassifisering
Når Cohens kappa er definert som ovenfor, tas det ikke hensyn til hvor stort avvik det er mellom observatørene når de er uenige. I eksemplet er klassifiseringen ordinal: Jo lenger unna diagonalen i tabell 1 man er, desto større er avviket mellom observatørene. Ved ordinale klasser er det mer relevant å bruke Cohens kvadratisk vektede kappa. Beregning av vektet kappa er f.eks. beskrevet hos Fagerland og medarbeidere (3, s. 551–552). I eksemplet fås en vektet kappa på 0,89, som er vesentlig høyere enn uvektet kappa. Dette er naturlig, da observatørene i nesten alle tilfellene avviker fra hverandre med maksimum én klasse.
Vektet kappa er ikke relevant hvis klassifiseringen er i bare to klasser, eller hvis klassene ikke representerer en ordinal skala. Hvis man bare var interessert i kategori I til III, versus kategori IV til V i eksemplet, ville krysstabellen bli som i tabell 2. Her er totalt samsvar lik po = (56 + 14) / 79 = 0,886, og samsvar ved tilfeldighet er lik pe = (57 · 64 + 22 · 15) / 792 = 0,637. Cohens kappa blir
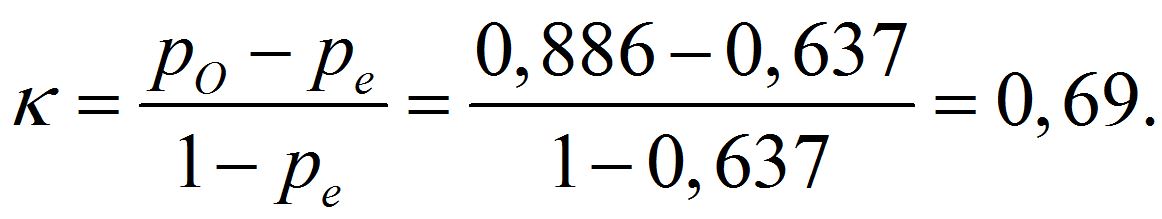
Tabell 2
Data fra tabell 1 slått sammen til to kategorier (2)
|
|
Observatør B
|
|
|
Observatør A
|
I-III
|
IV-V
|
Totalt
|
|
I-III
|
56
|
8
|
64
|
|
IV-V
|
1
|
14
|
15
|
|
Totalt
|
57
|
22
|
79
|
Begrensninger ved kappa
Verdien av kappa er sterkt avhengig av antall kategorier. Videre er Cohens kappa, i likhet med en korrelasjonskoeffisient, avhengig av hvor homogen populasjonen er: Dersom nesten alle observasjonene er i samme klasse, vil kappa bli liten, selv ved «godt» samsvar (3, s. 555).
Andre mål på samsvar
Andre mål på samsvar, som Aickin’s alpha og Gwet’s AC1, har ikke den sistnevnte svakheten, men er til gjengjeld vanskeligere å tolke (3, s. 552). Når vi har bare to kategorier, som frisk versus syk, kan det være mer relevant å beregne to mål på samsvar, nemlig positivt og negativt samsvar.
