Det er ofte av interesse å undersøke om effekten av en gitt eksponering er forskjellig i forskjellige grupper av individer – for eksempel om røyking har den samme effekten på risiko for hjertesykdom blant kvinner som blant menn. Dette kalles ofte effektheterogenitet.
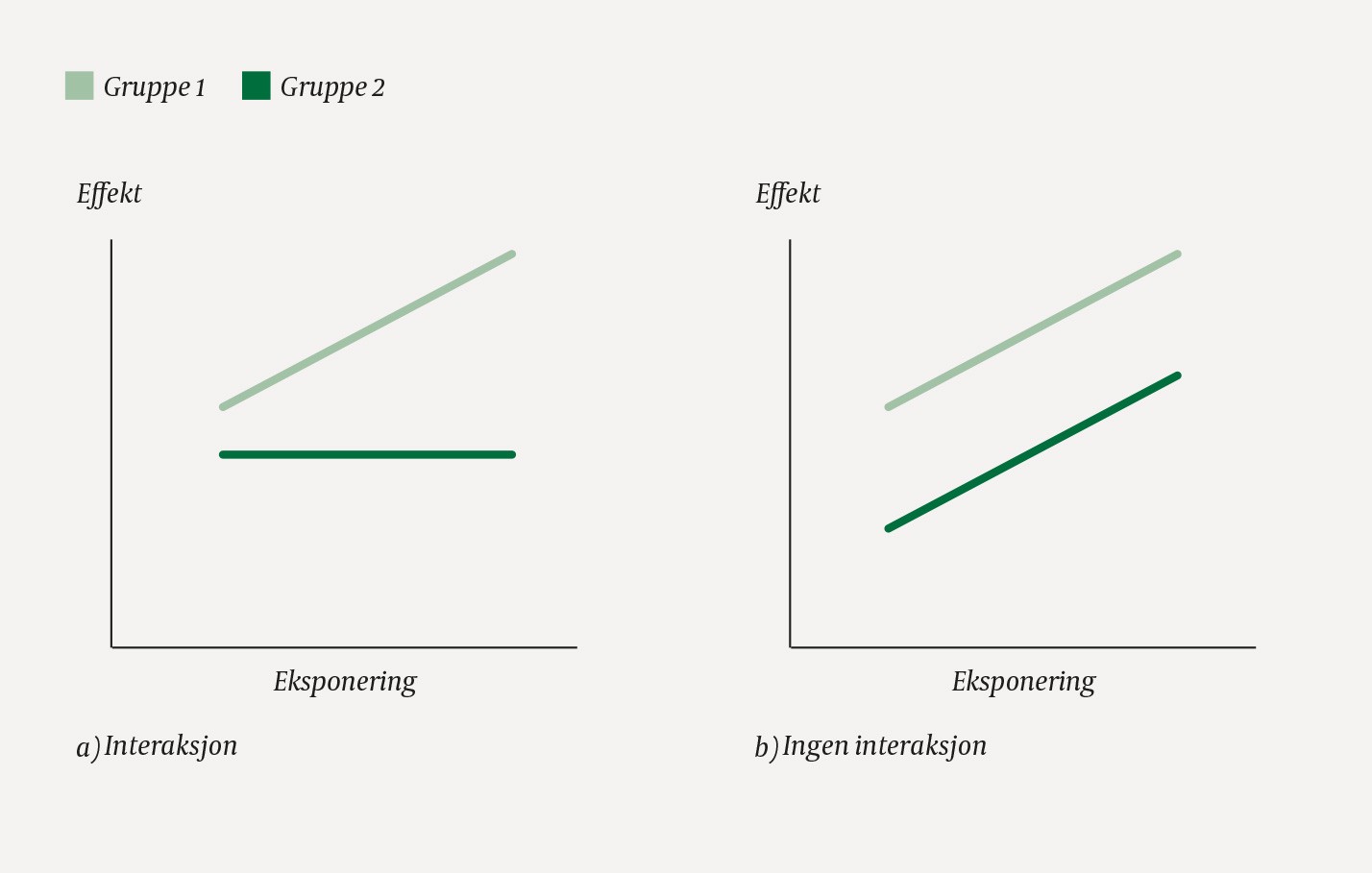
Illustrasjon av statistisk interaksjon. I a) er effekten av eksponeringen sterkere i gruppe 1, mens i b) er effekten av eksponeringen den samme i gruppe 1 og 2.
En naturlig fremgangsmåte vil være å analysere effekten separat blant kvinner og menn. Anta nå at vi finner en statistisk signifikant effekt blant menn, men ikke blant kvinner. Da er det nærliggende å konkludere med at effekten ikke er den samme. Dette er imidlertid en feilslutning. Det at vi har en statistisk signifikant effekt i den ene gruppen, men ikke i den andre, kan ikke brukes som argument for at de to effektene er signifikant forskjellige. En slik forskjell kan for eksempel skyldes at det var flere menn enn kvinner inkludert i studien, og vi vet at p-verdier er en funksjon av antall observasjoner. Mer fornuftig vil det være å sammenligne de estimerte effektene. Hvis den estimerte effekten blant menn er sterkere enn blant kvinner, er det igjen naturlig å konkludere med forskjell. Imidlertid må vi huske at disse effektene er estimert med noe usikkerhet, så selv om det er forskjell på de to estimatene, kan dette godt skyldes tilfeldigheter. Det er ikke gitt at den reelle effekten av røyking er forskjellig. Vi trenger en statistisk test.
Interaksjonstest
En generell metode for å teste effektforskjell er å gjennomføre en regresjonsanalyse med et interaksjonsledd. La oss anta at vi har estimert effekten av røyking ved hjelp av oddsforholdet (OR). En test på om de to estimerte oddsforholdene er signifikant forskjellige, får vi da ved å gjennomføre en logistisk regresjonsanalyse med hjertesykdom som utfall og hhv. røyking, kjønn og interaksjonen mellom disse som forklaringsvariabler. Interaksjonen mellom røyking og kjønn legger vi inn i modellen rett og slett ved å konstruere en ny variabel som ser ut som produktet av de to variablene røyking og kjønn. Modellen gir oss nå en test på om vi har en statistisk signifikant interaksjon, som er det samme som å si at effekten av røyking varierer signifikant mellom menn og kvinner.
Skalaavhengighet
La oss nå tenke oss at vi har følgende (høyst ikke-reelle) data som ligger til grunn for betraktningene over: Vi har 100 røykere og 100 ikke-røykere av begge kjønn. Blant mennene utvikler 20 av røykerne og 10 av ikke-røykerne hjertesykdom, mens blant kvinnene er de tilsvarende tallene 30 og 20. Beregner vi oddsforholdet, finner vi OR = 2,25 blant mennene og 1,71 blant kvinnene, altså en tilsynelatende svakere effekt av røyking blant kvinnene. La oss nå se på risikodifferansen som et alternativ til oddsforholdet. Denne finner vi ved å ta andelen røykere som utvikler hjertesykdom minus andel ikke-røykere som utvikler hjertesykdom. Blant menn finner vi 0,2 – 0,1 = 0,1 og blant kvinner finner vi 0,3 – 0,2 = 0,1. Her finner vi altså samme effekt av røyking blant kvinner som blant menn! Dette illustrerer at statistisk interaksjon/effektheterogenitet er skalaavhengig. Vi kan altså ha statistisk interaksjon på én skala, men ikke på en annen. Spesifikt vil det være slik at dersom det ikke er interaksjon på en lineær skala (risikodifferansen over), så vil det nødvendigvis være interaksjon på multiplikativ skala dersom begge de to faktorene som inngår i interaksjonen har en effekt på utfallet vårt. Interaksjonen vil selvfølgelig ikke nødvendigvis opptre som statistisk signifikant. Dette vil igjen være avhengig av utvalgsstørrelse og dermed statistisk styrke. Dette med skalaavhengighet vil ofte kunne forklare divergerende funn fra for eksempel en lineær og en logistisk regresjonsmodell.
Kombinert effekt av flere eksponeringer
I eksemplet over har vi primært vært interessert i effekten av én gitt eksponering (røyking) og vi har studert hvordan denne effekten har variert i forhold til nivå av en annen variabel (kjønn). Dette kalles også ofte for effektmodifisering. Dette er prinsipielt forskjellig fra situasjonen hvor vi har to eksponeringer og er interessert i effekten av å kombinere disse eksponeringene. Et klinisk eksempel på dette kan være at vi er interessert i den kombinerte effekten av to blodfortynnende medikamenter på risiko for hjertesykdom og vår primær interesse er om den kombinerte effekten er større enn summen av de to individuelle effektene. Den prinsipielle forskjellen består altså i at mens vi i eksemplet over primært var interessert i effekten av én gitt eksponering, er vi nå interessert i den kombinerte effekten av to eksponeringer. Fra et statistisk ståsted er det imidlertid ingen stor forskjell på disse to problemstillingene. Vi kan undersøke begge ved å inkludere et interaksjonsledd i en regresjonsmodell.
Multiplisitet
Når man analyserer en observasjonell studie, vil en regresjonsmodell fort inkludere en rekke variabler. Det kan da være fristende å lete etter alle mulige interaksjoner blant disse variablene. En slik fremgangsmåte er imidlertid ikke å anbefale, da man fort ender opp i problemer med tilfeldige funn (multippel testing-problemer). Man vil typisk anbefale at man undersøker de interaksjonene som a priori synes biologisk/klinisk plausible (1, s. 287).