I medisinsk forskning ønsker man ofte å studere sammenheng mellom to variabler. Den grunnleggende metoden for å svare på denne typen spørsmål er enkel lineær regresjon.
Med en enkel lineær regresjonsanalyse estimerer man sammenheng mellom et utfall målt på kontinuerlig skala og en forklaringsvariabel. Modellen tilpasser en rett linje (Y = a + bx) til et sett av parede observasjoner.
Figur 1 viser sammenheng mellom CRP-konsentrasjon i mg/L og livskvalitet målt med spørreskjemaet EORTC QLQ-C30 for 23 pasienter med metastatisk tarmkreft. Datapunktene er selektert fra en større studie med i alt 411 pasienter (1).
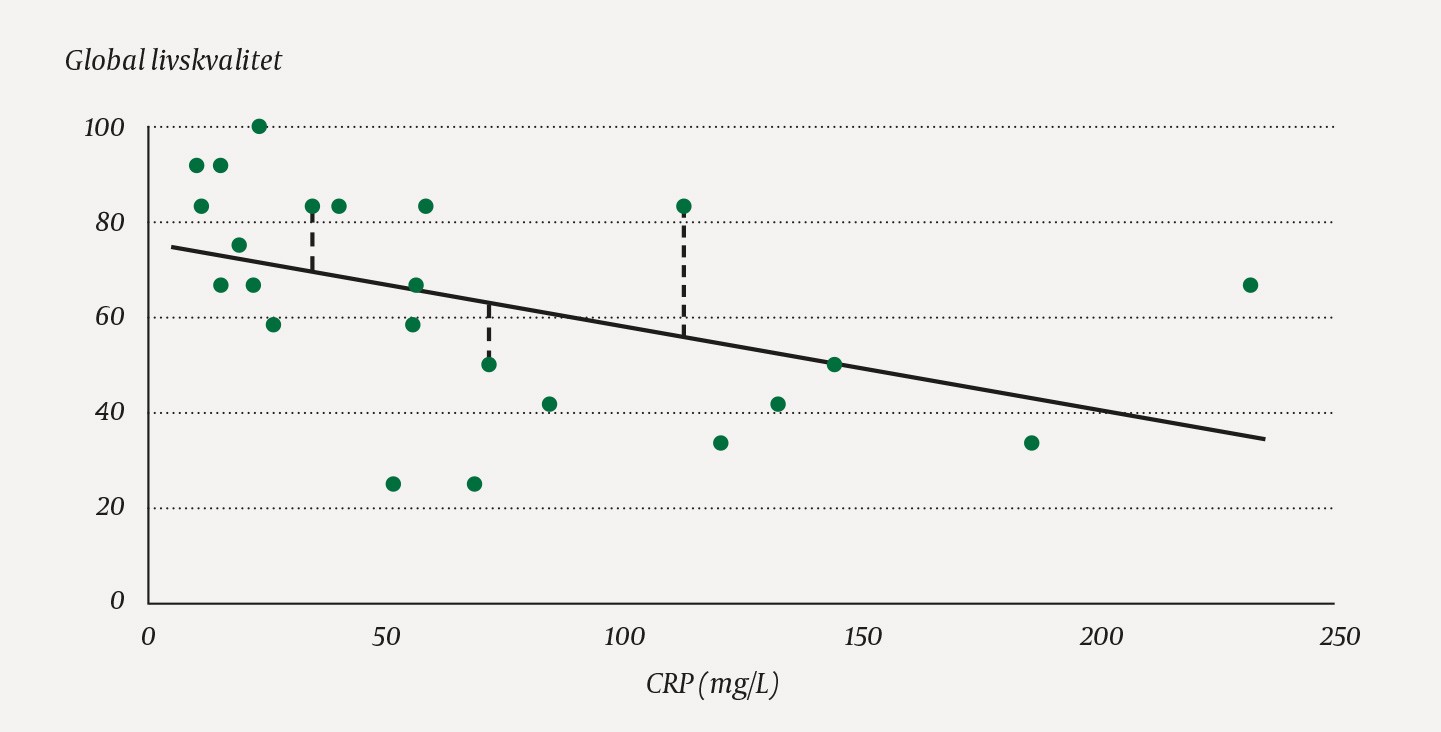
Figur 1 Sammenheng mellom CRP-konsentrasjon og livskvalitetsskår hos 23 pasienter med metastatisk tarmkreft (2). Stiplede vertikale linjer er eksempler på residualer.
Minste kvadraters metode
Det er sjelden at observerte data ligger langs en helt rett linje, og det kommer tydelig frem i eksemplet i figur 1. Vi ser en tendens til at livskvalitetsskåren faller med økende CRP, men det er en god del uforklart variasjon, altså en forskjell mellom observert verdi og den verdien modellen predikerer. Disse forskjellene kaller vi residualer.
Dersom det er en (tilnærmet) lineær sammenheng mellom to variabler, er utfordringen å finne den linjen som best beskriver sammenhengen. Denne estimeres ved minste kvadraters metode, der modellens parametere (konstantleddet a og stigningstallet b) bestemmes slik at summen av kvadratet av avstanden fra hvert enkelt datapunkt til den tilpassede linjen blir minst mulig. I figur 1 er residualene markert for tre av datapunktene.
Modellen
Det viktigste resultatet i en regresjonsanalyse er det estimerte stigningstallet, b. Med dette beregner man hvor sterk sammenhengen er. I eksemplet er estimert reduksjon i livskvalitetsskår 0,177 for hver enhet økning i CRP (b = −0,177). For å anslå usikkerheten i estimatet angir vi et 95 % konfidensintervall. I eksemplet er dette −0,329 til −0,025.
Ofte utføres også en signifikanstest som sammenligner det observerte stigningstallet med det man ville forvente under en nullhypotese om «ingen sammenheng» (b = 0). I eksemplet ble p-verdien 0,025, og det er statistisk signifikant sammenheng mellom CRP og livskvalitetsskår på 5 %-signifikansnivå.
I mange situasjoner er estimatet av konstantleddet a (verdien av Y når x = 0) ikke av interesse, enten fordi en x-verdi lik 0 ikke er biologisk relevant, eller fordi sammenhengen kun er lineær innenfor et begrenset område. Modellen er kun gyldig innenfor området der vi har målinger av den uavhengige variabelen. I eksemplet er konstantleddet a = 75,6. Det utnytter vi når vi vil predikere livskvalitetsskår: For en pasient med CRP = 50 er den predikerte verdien 75,6 + 50 · (−0,177) = 66,8.
Regresjonsanalysen kan brukes til å estimere hvor stor andel av variasjonen i utfallet som kan forklares av den uavhengige variabelen, såkalt forklart varians (r2). I eksemplet blir r2 = 0,22. Med andre ord er 22 % av variasjonen i livskvalitet forklart av CRP.
Antagelser
For at det skal gi mening å tilpasse en rett linje, må sammenhengen mellom variablene være tilnærmet lineær. Dette undersøkes ved hjelp av et spredningsdiagram, som vist i figur 1. Det er også nyttig å benytte (biologisk) forhåndskunnskap.
Residualene må være uavhengige. Denne antagelsen holder ikke hvis vi f.eks. har flere par av målinger fra samme individ. Videre skal residualene være tilnærmet normalfordelt rundt den tilpassede linjen. Denne antagelsen kan sjekkes ved hjelp av et histogram eller et normalfordelingsplott (2). Residualene skal også være uavhengige av den predikerte verdien.
Ekstremverdier kan påvirke de estimerte parameterne betydelig. De kan ikke uten videre fjernes, men man må kanskje vurdere om en enkel lineær modell virkelig passer. Kanskje kan man transformere data slik at antagelsene blir bedre oppfylt.
Andre regresjonsmodeller
I praksis er vi gjerne interessert i å inkludere flere forklaringsvariabler i en modell, såkalt multippel lineær regresjon. Forklaringsvariablene kan være skalavariabler, kategorivariabler eller dikotome variabler (ja/nei), eller en blanding av disse.
Det er ikke alltid slik at en utfallsvariabel måles på en kontinuerlig skala. Dersom utfallet er dikotomt, er f.eks. en logistisk regresjonsmodell egnet (3), og når vi analyserer levetider og har sensurerte observasjoner, kan Cox’ regresjonsmodell for proporsjonale hasarder passe. Disse modellene blir hyppig brukt i medisinsk forskning. Statistisk modellering er et stort fagfelt, men enkel lineær regresjon kan kanskje kalles alle regresjonsmodellers mor.
